Máquinas de soporte de vectores
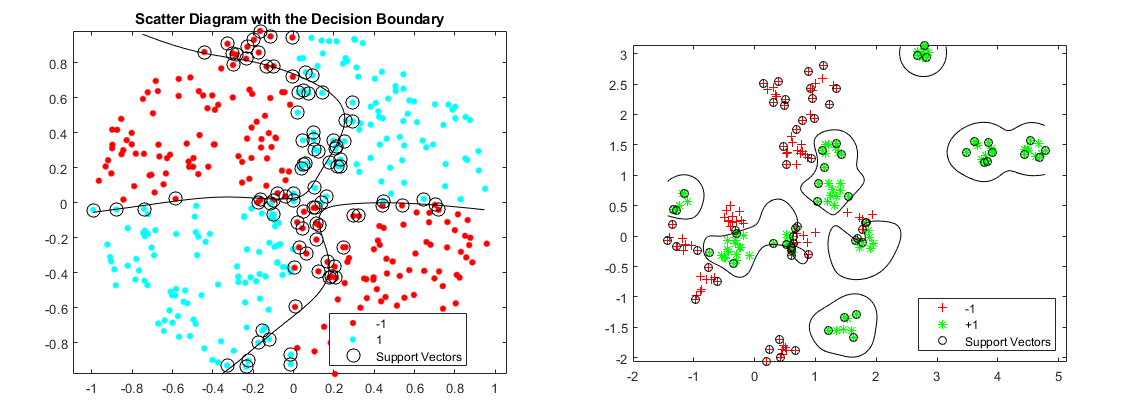
Las máquinas de soporte de vectores (SVM – Support Vector Machine) es un algoritmo supervisado que puede clasificar los casos mediante la búsqueda de un separador. SVM trabaja primero correlacionando datos con un espacio de características de alta dimensión para que los puntos de datos puedan ser categorizados, incluso cuando los datos no son de otro modo separables linealmente. A continuación, se estima un separador para los datos. Los datos deben ser transformados de tal manera que un separador pueda ser dibujado como un hiperplano.
La siguiente figura muestra la distribución de un conjunto pequeño de células en función del tamaño de la unidad y del grosor de la agrupación. Puede verse que los puntos de datos caen bajo dos categorías diferentes. Representa un conjunto de datos lineal y no separable. Las dos categorías se pueden separar con una curva, pero no con una línea. Es decir, representa un conjunto de datos linealmente no separable, que es el caso para la mayoría del conjunto de datos del mundo real.
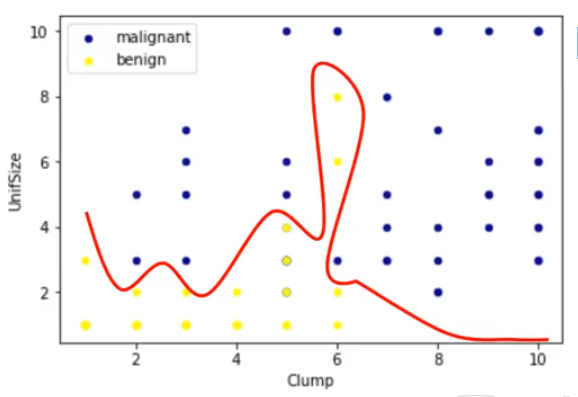
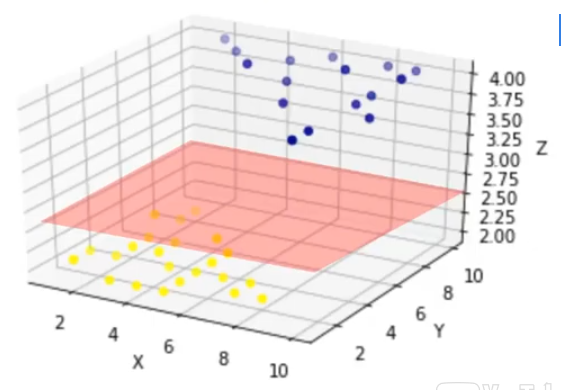
Pero podemos transferir estos datos a un espacio dimensional más alto, cómo por ejemplo a un espacio 3-dimensional. Después de la transformación, el límite entre las dos categorías se puede definir por un hiperplano. Como estamos ahora en un espacio tridimensional, el separador se muestra como un plano. Este plano se puede utilizar para clasificar casos nuevos o desconocidos. Por lo tanto, el algoritmo SVM tiene como resultado a un hiperplano óptimo que categoriza nuevos ejemplos.
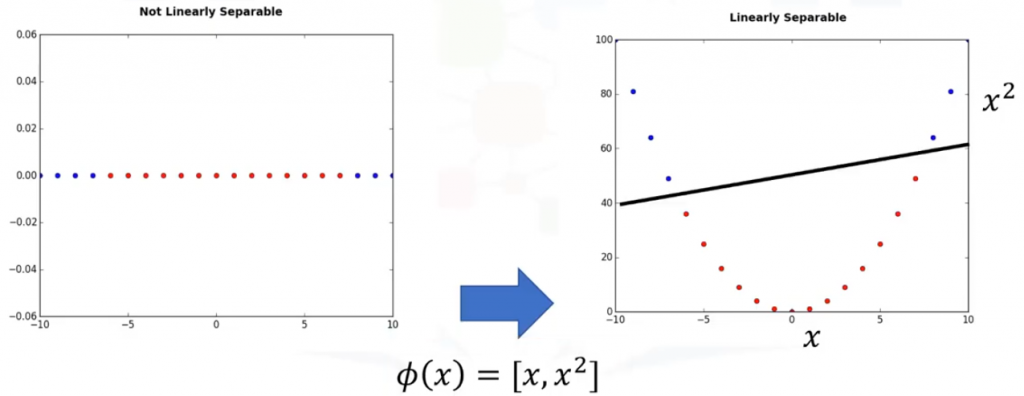
Transformación de los datos
Por simplificar vamos a imaginar que nuestro conjunto de datos esta conformado por datos uni-dimensionales, por lo que sólo tenemos una característica x y que no son linealmente separables. Podemos transferirlo a un espacio bidimensional, por ejemplo aumentando la dimensión de los datos correlacionando x en un nuevo espacio utilizando una función, con salidas x y x-cuadrado. Ahora, los datos son linealmente separables. Hay que tener en cuenta que estamos en un espacio bidimensional, por lo que el hiperplano es una línea que divide a un plano en dos partes donde cada clase se coloca en cada lado. Ahora podemos utilizar esta línea para clasificar los nuevos casos.
Básicamente, la correlación de datos en un espacio dimensional más alto se denomina kernelling. La función matemática utilizada para la transformación es conocida como la función kernel, y puede ser de diferentes tipos, como por ejemplo: Lineal, Polinomal, funcion Radial (o RBF) o Sigmoid. Cada una de estas funciones tiene sus propias características, sus pros y sus contras, y su ecuación, pero la buena noticia es que no necesitas conocerlos, ya que la mayoría de ellos ya están implementada en bibliotecas de lenguajes de programación de ciencia de datos. Además, como no es una forma fácil de saber qué función funciona mejor con cualquier conjunto de datos determinado, por lo general, elegimos diferentes funciones y comparamos los resultados. Puedes ver un ejemplo en este artículo: Máquinas de soporte de vectores en Python
Cómo encontrar el mejor separador de hiperplano después de la transformación
Las SVM se basan en la idea de encontrar un hiperplano que mejor divide un conjunto de datos en dos clases. Como estamos en un espacio bidimensional, se puede pensar en el hiperplano como una línea que linealmente separa unos puntos de los otros. Una elección razonable como el mejor hiperplano es la que representa la mayor separación, o margen, entre las dos clases. Por lo tanto, el objetivo es elegir un hiperplano con un margen tan grande como sea posible. Los ejemplos más cercanos al hiperplano son los vectores de soporte. Es intuitivo que sólo los vectores de apoyo importan para lograr nuestro objetivo y, por lo tanto, otros ejemplos de entrenamiento pueden ser ignorados. Tratamos de encontrar el hiperplano de tal manera que tenga la distancia máxima con respecto a los vectores de soporte. Hay que tener en cuenta que las líneas de decisión de hiperplano y límite tienen sus propias ecuaciones. Por lo tanto, encontrar el hiperplano optimizado se puede formalizar utilizando una ecuación que involucra un poco más de matemáticas. Dicho esto, el hiperplano se aprende de los datos de entrenamiento usando un procedimiento de optimización que maximiza el margen y al igual que muchos otros problemas,e ste problema de optimización también puede ser resuelto por el descenso de gradiente.
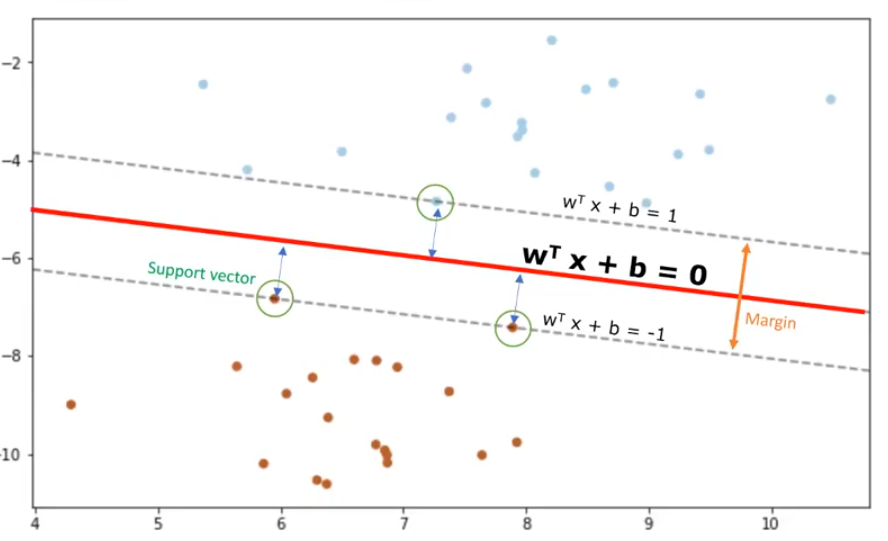
Por lo tanto, la salida del algoritmo es los valores ‘w’ y ‘b’ para la línea. Puede realizar clasificaciones utilizando esta línea estimada. Es suficiente aplicar los valores de entrada en la ecuación de la línea, entonces, se puede calcular si un punto desconocido está por encima o por debajo de la línea. Si la ecuación devuelve un valor mayor que 0, entonces el punto pertenece a la primera clase, que está por encima de la línea, y viceversa.
Las dos principales ventajas de las máquinas de vectores de soporte son que son exactas en espacios dimensionales altos y utilizan un subconjunto de puntos de entrenamiento en la función de decisión (llamados vectores de soporte), así que también es eficiente en el manejo de la memoria. Las desventajas de las máquinas de vectores de soporte incluyen el hecho de que el algoritmo es propenso para el exceso de ajuste, si el número de características es mucho mayor que el número de muestras. Además, las SVM no proporcionan directamente estimaciones de probabilidad, que son deseables en la mayoría de problemas de clasificación. Y, por último, las SVM no son muy eficientes computacionalmente, si su conjunto de datos es muy grande, como cuando tiene más de mil filas.
Situaciones donde utilizar máquinas de soporte de vectores
SVM es bueno para las tareas de análisis de imagen, como la clasificación de imagen de reconocimiento de dígitos escritos a mano. Además, SVM es muy eficaz en tareas de minería de textos, particularmente debido a su efectividad en el tratamiento de datos de alta dimensión. Por ejemplo, se utiliza para detectar spam, asignación de categorías de texto y análisis de sentimientos. Otra aplicación de SVM se encuentra en la clasificación de datos de Expresión de Gene, de nuevo, debido a su potencia en la clasificación de datos de alta dimensión. SVM también se puede utilizar para otros tipos de problemas de machine learning, tales como regresión, detección de valores atípicos,y agrupación en clúster.
Ir al artículo anterior de la serie: Cálculo de los parámetros de la función logística
Ir al artículo siguiente de la serie: Introducción al clustering
