función logística

Cálculo de los parámetros de la función logística

El objetivo principal es el cálculo de los parámetros de la función logística para que sea la mejor estimación de las etiquetas de las muestras en el conjunto de datos. Resumiendolo mucho, primero tenemos que mirar la función de costo y ver cuál es la relación entre la función de coste y los parámetros \theta. Por lo tanto, debemos formular la función de coste y usando su derivada podemos encontrar cómo cambiar los parámetros para reducir el costo, o mejor dicho, el error.

1. Búsqueda de la función de costo

Normalmente hay una ecuación general para calcular el costo que es la diferencia entre los valores reales de «y» y el resultado de nuestro modelo. Esta es una regla general para la mayoría de las funciones de coste en Machine Learning (aprendizaje automatizado). Podemos mostrarlo como el «Coste de nuestro modelo comparándolo con las etiquetas reales», o la «diferencia entre el
valor predicho de nuestro modelo y valor real del campo objetivo». Normalmente se usa el cuadrado de esa diferencia para evitar resultados negativos, y, por simplificar, la mitad de ese valor se considera como la función de coste:

Cost(\hat y, y)=\frac{1}{2}(\sigma(\theta^T X) - y)^2

Ahora, podemos escribir la función de costo para todas las muestras de nuestro conjunto de datos como la suma promedio de las funciones de coste de todos los casos. También se le llama error cuadrado medio (Mean Squared Error), y, como es una función de un parámetro vector θ, se muestra como J(θ).

J(\theta)=\frac{1}{m}\displaystyle\sum_{i-1}^{m}Cost(\hat y, y)

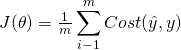
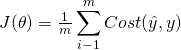
Para encontrar los mejores pesos o parámetros que minimizan esta función de coste deberíamos calcular el punto mínimo de esta función. Este punto mínimo se calcula utilizando la derivada, pero no hay una manera fácil de encontrarla para el punto mínimo global. La solución es encontrar otra función de coste en su lugar, una que tenga el mismo comportamiento pero sea más fácil para encontrar su punto mínimo.

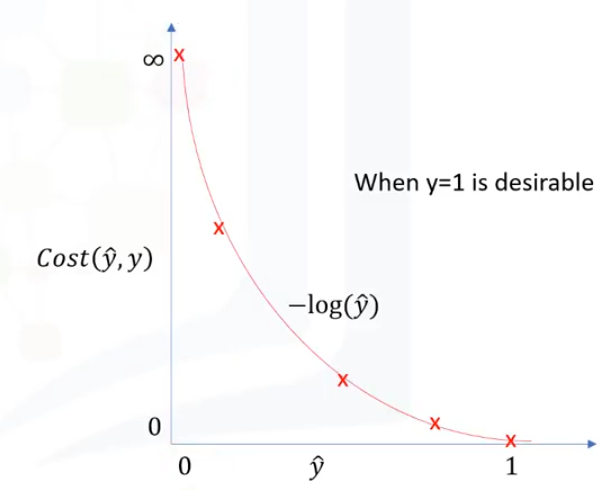
funcion -logRecordemos que nuestro modelo es \hat y, que el valor real es y (que es igual a 0 o 1) y que nuestro modelo trata de estimarlo. Vamos a suponer que el valor deseado para y es 1. Esto significa que nuestro modelo es mejor si estima y=1 y en ese caso la función de coste devería devolver 0, ya que es igual a la etiqueta real. El costo debería aumentar a medida que el resultado de nuestro modelo se aleje de 1, llegando a ser muy grande si el resultado de nuestro modelo es cercano a 0. Podemos ver que la función -log() proporciona tal función de coste. Por lo tanto, podemos usar la función -log() para calcular el costo de nuestro modelo de regresión logística. Ahora podemos conectarlo a nuestra función de costo total y reescribirlo como esta función. Por lo tanto, esta es la función de costo de regresión logística. Hay que recordar que \hat y no devuelve una clase como salida, sino que es un valor entre 0 y 1, lo que debe ser asumido como una probabilidad.

Cost(\hat y, y) = \left \{ \begin{matrix} -log(\hat y) & \mbox{si }y=1\\ -log(1 - \hat y) & \mbox{si }y=0\end{matrix}\right

J(\theta)=-\frac{1}{m}\displaystyle\sum_{i-1}^{m}y^{i}log(\hat y^i) + (1 - y^i)log(1 - \hat y^i)

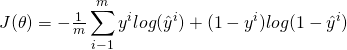
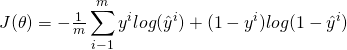
2. Minimización de la función de costo

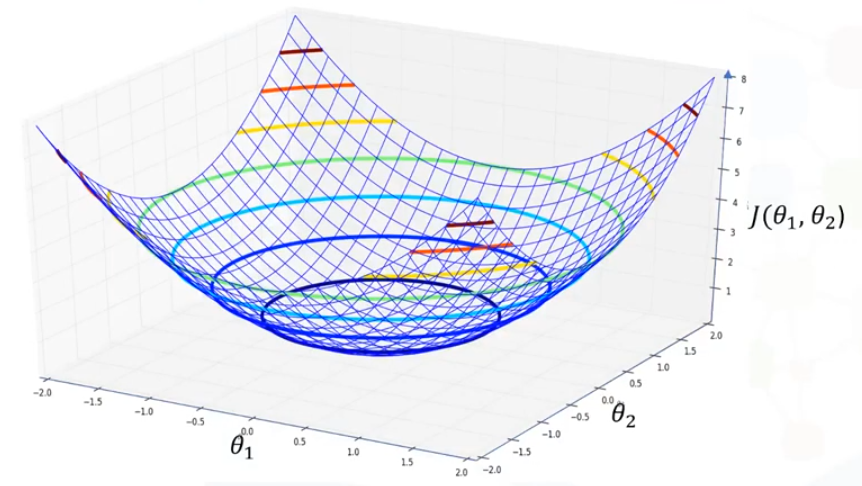
Para la minimización de la función de costo utilizamos un enfoque de optimización. Existen diferentes enfoques de optimización, pero vamos a utilizar uno de los más famosos y efectivos: el descenso gradual. Es un enfoque iterativo para encontrar el mínimo de la una función utilizando su derivada, así que con ella vamos a buscar el mínimo de la función de costo y así cambiar los valores de los parámetros, para minimizar el error.

Piense que los parámetros o pesos en nuestro modelo estan en un espacio bidimensional, por ejemplo, \theta_1, \theta_2, para 2 conjuntos de características, podrían ser edad e ingresos. Y tenemos una tercera dimensión que es el costo o error observado. Si trazamos la función de coste basada en todos los valores posibles de \theta_1, \theta_2, podemos ver algo como un tazón y representa el valor de error para diferentes valores de los parámetros. A esto se le llama «curva de error» o «tazón de error» de su función de costes. Ahora hay que buscar los valores de los parámetros que minimizan el valor de coste.
Se podría seleccionar valores de parámetros aleatorios que ubican un punto en el tazón y mientras que el valor del costo baje, podemos dar un paso más. También puede observarse que cuanto más empinada sea la pendiente, más lejos del punto mínimo estaremos, por lo que podremos elegir nuevos valores más lejos que los anteriores. Haciendo esto sucesivas veces y a medida que nos acercamos al punto más bajo, la pendiente disminuye, por lo que podemos dar pasos más pequeños hasta llegar a una superficie plana.

Para asegurarnos que descendemos, y qué los pasos son suficientemente grandes se debería calcular el gradiente de la función de coste en el punto estudiado. La derivada parcial de J(\theta) con respecto a cada parámetro en ese punto, da la pendiente del movimiento para cada parámetro en ese punto. Así que si nos movemos en la dirección opuesta a esa pendiente, garantizamos que bajamos en la curva de error. El valor del gradiente también indica el tamaño del paso a dar. Si la pendiente es grande, debemos dar un gran paso porque estamos lejos del mínimo y si la pendiente es pequeña deberíamos dar un paso más pequeño. El descenso en pendiente da pasos cada vez más pequeños hacia el mínimo con cada iteración. La derivada parcial de la función de coste J se calcula utilizando esta expresión.

\frac{\partial J}{\partial\theta_1}=-\frac{1}{m}\displaystyle\sum_{i=1}^{m}(y^i-\hat y^i)\hat y^i(1-\hat y^i)x_1

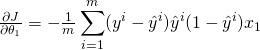
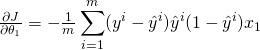
Esta ecuación devuelve la pendiente de ese punto, y deberíamos actualizar el parámetro en la dirección opuesta a la pendiente. Un vector de todas estas pendientes es el vector de gradiente:
\nabla J = \left [ \begin{matrix}\frac{\partial J}{\partial\theta_1} \\ \frac{\partial J}{\partial\theta_2} \\ \frac{\partial J}{\partial\theta_3} \\ \cdots \\ \frac{\partial J}{\partial\theta_k}\end{matrix} \right ]

Podemos usar este vector para cambiar o actualizar todos los parámetros, tomando los valores anteriores de los parámetros y restando la derivada de Error. Esto resulta en los nuevos parámetros para \theta que sabemos que disminuirá el costo: New \theta = old \theta - \nabla J. Además, si multiplicamos el valor del gradiente por un valor constante \eta, que se denomina velocidad de aprendizaje, tenemos un salto proporcional, dando un control adicional sobre la velocidad con la que nos movemos en la superficie: New \theta = old \theta - \eta\nabla J

En resumen, podemos decir simplemente que el descenso en pendiente es como dar pasos en la dirección actual de la pendiente, y el ritmo de aprendizaje es como la duración del paso que das. Así que, estos serían nuestros nuevos parámetros. Fíjate que es una operación iterativa y, en cada iteración, actualizamos los parámetros y minimizamos el coste, hasta que el algoritmo converge en un mínimo aceptable.

Recapitulando:

  • Paso 1. Inicializamos los parámetros con valores aleatorios.
  • Paso 2. Alimentamos la función de costes con la función y calcular el costo. Esperamos una alta tasa de error ya que los parámetros se establecen al azar.
  • Paso 3. Calculamos el gradiente del coste teniendo en cuenta que tenemos que usar una derivada parcial. Entonces, para calcular el vector de gradiente, necesitamos todos los datos de entrenamiento para alimentar la ecuación para cada parámetro. Por supuesto, esta es una parte costosa del algoritmo pero hay algunas soluciones para esto.
  • Paso 4. Las ponderaciones se actualizan con nuevos valores de parámetros.
  • Paso 5. Aquí volvemos al paso 2 y volvemos a alimentar la función de costes, que tiene nuevos parámetros. Esperamos menos errores a medida que vamos bajando por la superficie de los errores. Continuamos este ciclo hasta que alcanzamos un valor corto de costo, o un número limitado de iteraciones.
  • Paso 6. Los parámetros deben ser encontrados después de algunas iteraciones. Esto significa que el modelo está listo y podemos usarlo para predecir la probabilidad de que una observación pertenezca o no a una categoría.

Resulta obvio que todos estos pasos pueden realizarse mediante programas y sus librerias, puedes ver un ejemplo en este artículo: Regresión logística en Python

Ir al artículo anterior de la serie: Regresión lineal Vs. regresión logística

Ir al artículo siguiente de la serie: Máquinas de soporte de vectores

Artículos relacionadosMás del autor

DEJA UNA RESPUESTA

Por favor ingrese su comentario!
Por favor ingrese su nombre aquí