Vamos a crear un modelo basado en datos de telecomunicaciones para predecir cuándo los clientes buscarán otro competidor de tal forma que podamos tomar alguna decisión para retenerlos.

¿Cuál es la diferencia entre Regresión Logística y Regresión Lineal?

Mientras la Regresión Lineal es para estimar valores continuos (ej. estimar precios de casas), no es la mejor herramienta para predecir la clase de un punto de datos observados. Para estimar la clase de punto de datos, necesitaremos una guía de lo que sería la clase más probable para ese punto de datos. Por esto, utilizamos Regresión Logística.

Regresión Lineal:

Como sabes, la Regresión lineal encuentra una función que relaciona una variable continua dependiente, y, con algunos predictores (variables independientes x_1, x_2, etc.). Por ejemplo, la regresión lineal Simple asume una función de la forma:

y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots

y encuentra los valores de los parámetros \theta_0, \theta_1, \theta_2, etc, donde el término \theta_0 es «intersección». Generalmente se muestra como:

h_\theta(x)=\theta^T X

La Regresion Logística es una variación de una Regresión Lineal, útil cuando la variable dependiente observada, y, es categórica. Produce una fórmula que predice la probabilidad de la clase etiqueta como una función de las variables independientes.

La regresión logística es una curva especial en forma de s a partir de tomar la regresión lineal y transformar la estimación numérica en una probabilidad con la siguiente función, llamada sigmoide \sigma:

h_\theta(x)=\sigma(\theta^T X)=\frac{e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots)}}{1 + e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots)}}

O también: ProbabilidadDeUnaClase_1 = P(Y = 1 \vert X) = \sigma(\theta^T X) = \frac{e^{\theta^T X}}{1 + e^{\theta^T X}}

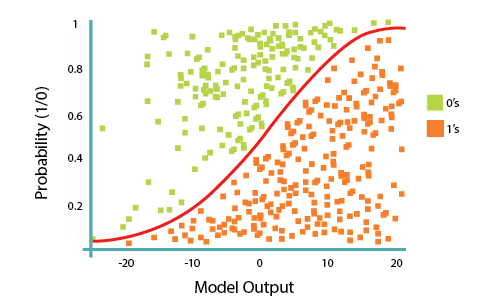
En esta ecuación, \theta^T X es el resultado de la regresión (la suma de las variables ponderadas por los coeficientes), e es la función exponencial y \sigma(\theta^T X) es la función sigmoide ó función logística, también llamada curva logística. Tiene una forma de «S» (curva sigmoide). En resumen, la Regresión Logística pasa la entrada a través de las funciones logística/sigmoide pero en realidad termina tratando al resultado como una probabilidad:
curva sigmoide

El objetivo del algoritmo de Regresión Logística, es encontrar los mejores parámetros \theta, para h_\theta (x) = \sigma(\theta^T X), de forma tal de que el modelo prediga lo mejor posible la clase de cada caso.

Cliente churn con Regresión Logística

Una compañía de telecomunicaciones está preocupada por el número de clientes que dejan sus líneas fijas de negocio por las de competidores de cable. Ellos necesitan entender quién se está yendo. Imagina que eres un analista en esta compañía y que tienes que descubrir quién es el cliente que se va y por qué

Primero, importemos las librerías necesarias:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
import pandas as pd
import pylab as pl
import numpy as np
import scipy.optimize as opt
from sklearn import preprocessing
%matplotlib inline
import matplotlib.pyplot as plt
[/sourcecode]

Acerca del conjunto de datos

Utilizaremos datos de las telecomunicaciones para poder predecir el cliente cancelador (churn). Estos son datos históricos de clientes donde cada fila representa un cliente. Los datos son fáciles de comprender, y podrás descubrir conclusiones que puedes usar de inmediato. Generalmente, es menos caro mantener clientes que conseguir nuevos, así que el foco de este análisis es predecir los clientes que se quedarían en la compañía.
Estos datos proveen información que ayudarán a predecir comportamientos que retendrán a los clientes. Puedes analizar toda la información relevante del cliente y desarrollar programas de retención centrados en los clientes.

Los datos incluyen información acerca de:

  • Clientes que se fueron el último mes – la columna se llama Churn
  • Los servicios que cada cliente ha contratado – teléfono, líneas múltiples, internet, seguridad online, resguardo online, protección de dispositivos, soporte técnico y streaming de TV y películas
  • Información de la cuenta del cliente – cuánto hace que es cliente, contrato, método de pago, facturación digital, cargos mensuales y cargos totales
  • Información demográfica de los clientes – sexo, rango de edad y si tienen pareja y dependientes

Cargar los datos «Cancelaciones» de la Telco

«Telco Churn» es un archivo de datos ficticio que trata sobre los esfuerzos de una compañía de telecomunicaciones para reducir la huída de sus clientes. Cada caso corresponde a un cliente y se guarda información demográfica e información referente al uso del servicio. Antes de trabajar con los datos, debes utilizar la URL para obtener el archivo ChurnData.csv. Para descargarlo, utilizaremos !wget desde IBM Object Storage.

[sourcecode language=»python» wraplines=»false» collapse=»false»]
!wget -O ChurnData.csv https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/ChurnData.csv
[/sourcecode]

--2020-02-12 16:42:15--  https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/ChurnData.csv
Resolving s3-api.us-geo.objectstorage.softlayer.net (s3-api.us-geo.objectstorage.softlayer.net)... 67.228.254.196
Connecting to s3-api.us-geo.objectstorage.softlayer.net (s3-api.us-geo.objectstorage.softlayer.net)|67.228.254.196|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 36144 (35K)

[text language=»/csv»][/text]

Saving to: ‘ChurnData.csv’

ChurnData.csv 100%[===================>] 35.30K –.-KB/s in 0.02s

2020-02-12 16:42:15 (1.56 MB/s) – ‘ChurnData.csv’ saved [36144/36144]

Cargar los Datos desde el Archivo CSV

[sourcecode language=»python» wraplines=»false» collapse=»false»]
churn_df = pd.read_csv("ChurnData.csv")
churn_df.head()
[/sourcecode]

tenure age address income ed employ equip callcard wireless longmon … pager internet callwait confer ebill loglong logtoll lninc custcat churn
0 11.0 33.0 7.0 136.0 5.0 5.0 0.0 1.0 1.0 4.40 … 1.0 0.0 1.0 1.0 0.0 1.482 3.033 4.913 4.0 1.0
1 33.0 33.0 12.0 33.0 2.0 0.0 0.0 0.0 0.0 9.45 … 0.0 0.0 0.0 0.0 0.0 2.246 3.240 3.497 1.0 1.0
2 23.0 30.0 9.0 30.0 1.0 2.0 0.0 0.0 0.0 6.30 … 0.0 0.0 0.0 1.0 0.0 1.841 3.240 3.401 3.0 0.0
3 38.0 35.0 5.0 76.0 2.0 10.0 1.0 1.0 1.0 6.05 … 1.0 1.0 1.0 1.0 1.0 1.800 3.807 4.331 4.0 0.0
4 7.0 35.0 14.0 80.0 2.0 15.0 0.0 1.0 0.0 7.10 … 0.0 0.0 1.0 1.0 0.0 1.960 3.091 4.382 3.0 0.0

Selección y pre-procesamiento de datos

Seleccionemos algunas características para el modelado. También cambiemos el tipo de dato del objetivo (target) para que sea un número entero (integer), ya que es un requerimiento del algoritmo skitlearn:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
churn_df = churn_df[[‘tenure’, ‘age’, ‘address’, ‘income’, ‘ed’, ‘employ’, ‘equip’, ‘callcard’, ‘wireless’,’churn’]]
churn_df[‘churn’] = churn_df[‘churn’].astype(‘int’)
churn_df.head()
[/sourcecode]

tenure age address income ed employ equip callcard wireless churn
0 11.0 33.0 7.0 136.0 5.0 5.0 0.0 1.0 1.0 1
1 33.0 33.0 12.0 33.0 2.0 0.0 0.0 0.0 0.0 1
2 23.0 30.0 9.0 30.0 1.0 2.0 0.0 0.0 0.0 0
3 38.0 35.0 5.0 76.0 2.0 10.0 1.0 1.0 1.0 0
4 7.0 35.0 14.0 80.0 2.0 15.0 0.0 1.0 0.0 0

[sourcecode language=»python» wraplines=»false» collapse=»false»]
churn_df.describe()
[/sourcecode]

tenure age address income ed employ equip callcard wireless churn
count 200.000000 200.000000 200.000000 200.000000 200.00000 200.00000 200.000000 200.000000 200.000000 200.000000
mean 35.505000 41.165000 11.650000 75.130000 2.82500 10.22500 0.425000 0.705000 0.290000 0.290000
std 21.640971 13.076803 10.158419 128.430468 1.28555 8.95743 0.495584 0.457187 0.454901 0.454901
min 1.000000 19.000000 0.000000 9.000000 1.00000 0.00000 0.000000 0.000000 0.000000 0.000000
25% 16.750000 31.000000 3.000000 31.000000 2.00000 3.00000 0.000000 0.000000 0.000000 0.000000
50% 33.500000 40.000000 9.000000 48.000000 3.00000 7.50000 0.000000 1.000000 0.000000 0.000000
75% 55.250000 51.000000 18.000000 80.000000 4.00000 17.00000 1.000000 1.000000 1.000000 1.000000
max 72.000000 76.000000 48.000000 1668.000000 5.00000 44.00000 1.000000 1.000000 1.000000 1.000000

Definamos X, e y para nuestro set de datos:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
X = np.asarray(churn_df[[‘tenure’, ‘age’, ‘address’, ‘income’, ‘ed’, ‘employ’, ‘equip’]])
X[0:5]
[/sourcecode]

array([[ 11.,  33.,   7., 136.,   5.,   5.,   0.],
       [ 33.,  33.,  12.,  33.,   2.,   0.,   0.],
       [ 23.,  30.,   9.,  30.,   1.,   2.,   0.],
       [ 38.,  35.,   5.,  76.,   2.,  10.,   1.],
       [  7.,  35.,  14.,  80.,   2.,  15.,   0.]])

[sourcecode language=»python» wraplines=»false» collapse=»false»]
y = np.asarray(churn_df[‘churn’])
y [0:5]
[/sourcecode]

array([1, 1, 0, 0, 0])

También, normalicemos el set de datos:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
X[0:5]
[/sourcecode]

array([[-1.13518441, -0.62595491, -0.4588971 ,  0.4751423 ,  1.6961288 ,
        -0.58477841, -0.85972695],
       [-0.11604313, -0.62595491,  0.03454064, -0.32886061, -0.6433592 ,
        -1.14437497, -0.85972695],
       [-0.57928917, -0.85594447, -0.261522  , -0.35227817, -1.42318853,
        -0.92053635, -0.85972695],
       [ 0.11557989, -0.47262854, -0.65627219,  0.00679109, -0.6433592 ,
        -0.02518185,  1.16316   ],
       [-1.32048283, -0.47262854,  0.23191574,  0.03801451, -0.6433592 ,
         0.53441472, -0.85972695]])

Entrenar/Probar el set de datos

Ahora, dividamos nuestro set de datos en dos sets, entrenamiento y prueba:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print (‘Train set:’, X_train.shape, y_train.shape)
print (‘Test set:’, X_test.shape, y_test.shape)
[/sourcecode]

Train set: (160, 7) (160,)
Test set: (40, 7) (40,)

Modelando (Regresión Logística con Scikit-learn)

Construyamos nuestro modelo utilizando LogisticRegression con el package Scikit-learn. Esta función implementa regresión logística y puede usar distintos optimizadores numéricos para encontrar parámetros, a saber, ‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’ solvers. Puedes también encontrar más información sobre los pros y contras de estos optimizadores si buscas en internet.

La versión de Regresión Logística soporta regularización. Esto es, una técnica que soluciona problemas de sobreajuste en modelos de machine learning. El parámetro C indica fuerza de regularización inversa la cual debe ser un número flotante positivo. Valores más pequeños indican regularización más fuerte. Llenemos nuesto modelo con el subconjunto de entrenamiento:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
LR = LogisticRegression(C=0.01, solver=’liblinear’).fit(X_train,y_train)
LR
[/sourcecode]

LogisticRegression(C=0.01, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='warn',
          n_jobs=None, penalty='l2', random_state=None, solver='liblinear',
          tol=0.0001, verbose=0, warm_start=False)

Ahora, podremos predecir usando nuestro set de prueba:

[sourcecode language=»python» wraplines=»false» collapse=»false»]
yhat = LR.predict(X_test)
yhat
[/sourcecode]

array([0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0])

predict_proba devuelve estimaciones para todas las clases. La primer columna es la probabilidad de la clase 1, P(Y=1|X), y la segunda columna es la probabilidad de la clase 0, P(Y=0|X):

[sourcecode language=»python» wraplines=»false» collapse=»false»]
yhat_prob = LR.predict_proba(X_test)
yhat_prob
[/sourcecode]

array([[0.54132919, 0.45867081],
       [0.60593357, 0.39406643],
       [0.56277713, 0.43722287],
       [0.63432489, 0.36567511],
       [0.56431839, 0.43568161],
       [0.55386646, 0.44613354],
       [0.52237207, 0.47762793],
       [0.60514349, 0.39485651],
       [0.41069572, 0.58930428],
       [0.6333873 , 0.3666127 ],
       [0.58068791, 0.41931209],
       [0.62768628, 0.37231372],
       [0.47559883, 0.52440117],
       [0.4267593 , 0.5732407 ],
       [0.66172417, 0.33827583],
       [0.55092315, 0.44907685],
       [0.51749946, 0.48250054],
       [0.485743  , 0.514257  ],
       [0.49011451, 0.50988549],
       [0.52423349, 0.47576651],
       [0.61619519, 0.38380481],
       [0.52696302, 0.47303698],
       [0.63957168, 0.36042832],
       [0.52205164, 0.47794836],
       [0.50572852, 0.49427148],
       [0.70706202, 0.29293798],
       [0.55266286, 0.44733714],
       [0.52271594, 0.47728406],
       [0.51638863, 0.48361137],
       [0.71331391, 0.28668609],
       [0.67862111, 0.32137889],
       [0.50896403, 0.49103597],
       [0.42348082, 0.57651918],
       [0.71495838, 0.28504162],
       [0.59711064, 0.40288936],
       [0.63808839, 0.36191161],
       [0.39957895, 0.60042105],
       [0.52127638, 0.47872362],
       [0.65975464, 0.34024536],
       [0.5114172 , 0.4885828 ]])

Evaluación

Índice jaccard

Probemos con el índice jaccard para la evaluación de precisión. Podemos definir como jaccard al tamaño de la intersección dividida por el tamaño de la unión de dos set de etiquetas. Si todo el set de etiquetas de muestra predichas coinciden con el set real de etiquetas, entonces la precisión es 1.0; sino, sería 0.0.

[sourcecode language=»python» wraplines=»false» collapse=»false»]
from sklearn.metrics import jaccard_similarity_score
jaccard_similarity_score(y_test, yhat)
[/sourcecode]

0.75

Matriz de confusión

Otra forma de mirar la precisión del clasificador es ver la matriz de confusión.

[sourcecode language=»python» wraplines=»false» collapse=»false»]
from sklearn.metrics import classification_report, confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes, normalize=False, title=’Confusion matrix’, cmap=plt.cm.Blues):
"""
Esta función muestra y dibuja la matriz de confusión.
La normalización se puede aplicar estableciendo el valor `normalize=True`.
"""
if normalize:
cm = cm.astype(‘float’) / cm.sum(axis=1)[:, np.newaxis]
print("Matriz de confusión normalizada")
else:
print(‘Matriz de confusión sin normalización’)

print(cm)

plt.imshow(cm, interpolation=’nearest’, cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)

fmt = ‘.2f’ if normalize else ‘d’
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt), horizontalalignment="center", color="white" if cm[i, j] > thresh else "black")

​ plt.tight_layout()
plt.ylabel(‘Etiqueta Real’)
plt.xlabel(‘Etiqueta Predicha’)
print(confusion_matrix(y_test, yhat, labels=[1,0]))
[/sourcecode]

[[ 6  9]
 [ 1 24]]

[sourcecode language=»python» wraplines=»false» collapse=»false»]
# Calcular la matriz de confusión
cnf_matrix = confusion_matrix(y_test, yhat, labels=[1,0])
np.set_printoptions(precision=2)

​# Dibujar la matriz de confusión no normalizada
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=[‘churn=1′,’churn=0′],normalize= False, title=’Matriz de confusión’)
[/sourcecode]

Matriz de confusión sin normalización
[[ 6  9]
 [ 1 24]]

Observa la primer fila. Ahí están los clientes cuyo valor churn en el set de prueba es 1. Como podrás calcular, de 40 clientes, el valor churn de 15 de ellos es 1. Y de otros 15, el clasificador predijo que 6 de ellos son 1 y 9 0.
Quiere decir que, para 6 clientes, el valor actual de churn fue 1 en el set de pruebas y el clasificador los predijo correctamente como 1. Sin embargo, mientras la etiqueta actual de 9 clientes era 1, el clasificador los predijo como 0, lo cual no es muy bueno. Lo podemos considerar como un error del modelo para la primer fila.
¿Qué pasa con los clientes con valor churn 0? Miremos la segunda fila. Parece que hay 25 clientes con valor churn 0.
El clasificador predijo correctamente 24 de ellos como 0 y uno de ellos equivocadamente como 1. Así que ha hecho un buen trabajo prediciendo los clientes con churn 0. Una ventaja de la matriz de confusión es que muestra la abilidad del modelo para correctamente predecir o separar las clases. En el caso de clasificador binario, como el ejemplo, podemos entender a estos números como la cantidad de positivos verdaderos, negativos verdaderos y negativos falsos.

[sourcecode language=»python» wraplines=»false» collapse=»false»]
print (classification_report(y_test, yhat))
[/sourcecode]

              precision    recall  f1-score   support

           0       0.73      0.96      0.83        25
           1       0.86      0.40      0.55        15

   micro avg       0.75      0.75      0.75        40
   macro avg       0.79      0.68      0.69        40
weighted avg       0.78      0.75      0.72        40

​
Partiendo de la cantidad de cada sección podemos calcular la precisión y el grado(recall) de cada etiqueta:

  • Precision es una medida de certeza basada en una etiqueta predicha. Se define de esta forma: precision = TP / (TP + FP)
  • Recall es un grado positivo verdadero. Se define de esta forma: Recall = TP / (TP + FN)

Por lo tanto, podemos calcular la precisión y grado de cada clase.

F1 score: Ahora estamos en condiciones de calcular los puntajes F1 para cada etiqueta basada en la precisión y grado de cada etiqueta.

El puntaje F1 es el promedio armónico de la precisión y grado, donde un grado F1 alcanza su mejor valor en 1 (precisión y grado perfectos) y peor escenario en 0. Es una buena forma de mostrar que un clasificador tiene un buen valor tanto para la precisión como para el grado.

Y finalmente, podemos decir que la exactitud promedio para este clasificador es el promedio del score f1 para ambas etiquetas, cuyo valor es is 0.72 en nuestro caso.

log loss

Ahora, probemos log loss para la evaluación. En regresión logística, la salida puede ser que la probabilidad de cliente churn sea sí (o su equivalente 1). Esta probabilidad es un valor entre 0 y 1. Log loss( pérdida logarítmica) mida el rendimiento de un clasificador donde la salida predicha es una probabilidad de valor entre 0 y 1.

[sourcecode language=»python» wraplines=»false» collapse=»false»]
from sklearn.metrics import log_loss
log_loss(y_test, yhat_prob)
[/sourcecode]

0.6017092478101185

Modelo con valores diferentes

Vamos a construir el modelo de Regresión Logística de nuevo para el mismo set de datos, pero esta vez, utilizando valores diferentes de solucionador y regularización.

[sourcecode language=»python» wraplines=»false» collapse=»false»]
LR2 = LogisticRegression(C=0.01, solver=’sag’).fit(X_train,y_train)
yhat_prob2 = LR2.predict_proba(X_test)
print ("LogLoss: : %.2f" % log_loss(y_test, yhat_prob2))
[/sourcecode]

LogLoss: : 0.61

Artículos relacionadosMás del autor

DEJA UNA RESPUESTA

Por favor ingrese su comentario!
Por favor ingrese su nombre aquí