Regresión lineal múltiple
Regresión lineal múltiple
La regresión lineal múltiple es la extensión de el modelo de regresión lineal simple.
Este tipo de regresión puede utilizarse cuando queremos...
Regresión lineal en R
Regresión simple
require(MASS) # importa la libreria MASS con funciones y métodos estadísticos
require(ISLR) # importa la librería ISLR con datos para un aprender estadística con...
Regresión lineal en Pyton
Importación de los paquetes básicos
import matplotlib.pyplot as plt # para crear graficos
import pandas as pd ...
Regresión lineal simple
Regresión lineal simple
La pregunta que trata de responder la regresión linea simple es: Dado un conjunto de datos, ¿Podemos predecir una de las variables,...
Introducción al Modelo de Regresión
Introducción al modelo de regresión.
Para la introducción al modelo de regresión, vamos a utilizar el conjunto de datos que se muestra. Estos estan relacionados...
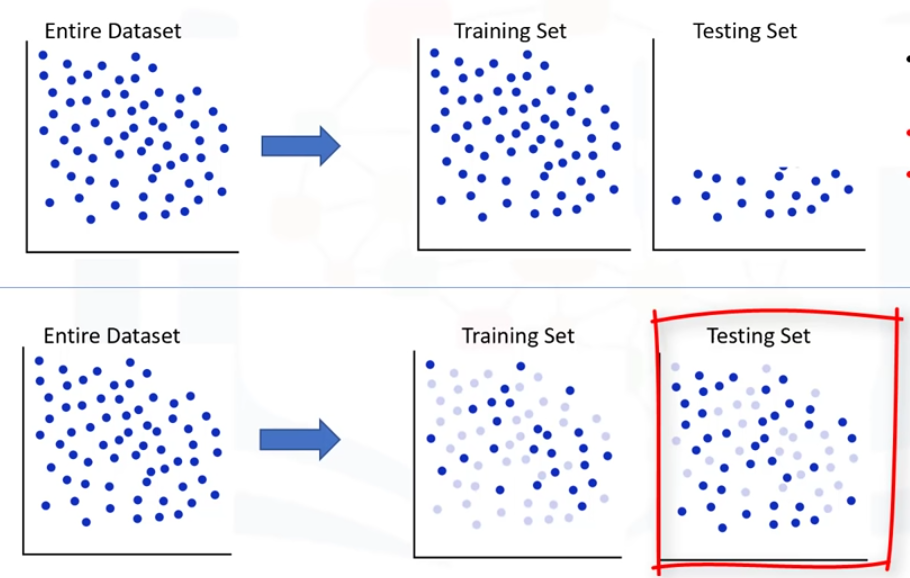
Aprendizaje Supervisado y No Supervisado
Aprendizaje supervisado
Una manera fácil de empezar a entender el concepto de aprendizaje supervisado es observando directamente a las palabras que lo componen: Supervisado significa...