K-vecinos más próximos
Para comprender el algorítmo de clasificación K-vecinos más próximos, imagine que un proveedor de telecomunicaciones ha segmentado su base de clientes según el patrón de uso de servicios, categorizando a los clientes en cuatro grupos. Si los datos demográficos se pueden utilizar para predecir la pertenencia a un grupo, la empresa puede personalizar ofertas para clientes potenciales. Se trata de un problema de clasificación. Es decir, dado el conjunto de datos, con las etiquetas predefinidas, tenemos que construir un modelo que se utilizará para predecir la clase de un caso nuevo o desconocido. El ejemplo se centra en el uso de datos demográficos, como la región, la edad y el estado civil, para predecir patrones de uso. El campo objetivo, tiene cuatro valores posibles que corresponden a los cuatro grupos de clientes: Servicio básico, servicio electrónico, servicio adicional y servicio total. Nuestro objetivo es construir un clasificador usando datos de clientes conocidos para predecir el grupo de un nuevo cliente.
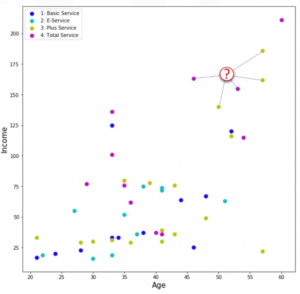
Vamos a utilizar el criterio de clasificación llamado «vecino más próximo». Para simplificar vamos a utilizar sólo dos campos como predictores, la Edad y el Salario, y luego pintar a los clientes en función de estos datos. Si ahora tenemos un nuevo cliente con una edad y salario conocido. ¿Cómo podemos encontrar la clase de este cliente? ¿Podemos encontrar uno de los casos más próximos y asignar la misma etiqueta de clase a nuestro nuevo cliente? ¿Podemos también decir que la clase de nuestro nuevo cliente es probablemente el mismo que el vecino más próximo? Sí, podemos. Pero ¿Hasta qué punto podemos confiar en nuestro juicio, que se basa en el el primer vecino más próximo? Podría ser un mal juicio, especialmente si el primer vecino más próximo es muy específico o un valor atípico, ¿correcto? Por esto, en lugar de elegir al primer vecino más próximo, ¿qué tal si elegimos a los cinco vecinos más próximos, y vemos que tipo es el más frecuente para definir la clase de nuestro nuevo cliente? ¿Esto no tiene más sentido? De hecho, sí.
Este ejemplo pone de relieve la intuición detrás del algoritmo del vecino más próximo.
Definición
El algoritmo del k-vecinos más próximos es un algoritmo de clasificación que toma un montón de puntos marcados y los utiliza para aprender a etiquetar otros puntos. Este algoritmo clasifica los casos basados en su similitud con otros casos. En los vecinos más próximos, los puntos de datos que están cerca entre sí se dicen que son «vecinos». El algoritmo se basa en este paradigma: Casos similares con las mismas etiquetas de clase están cerca el uno al otro.
Por lo tanto, la distancia entre dos casos es una medida de su disimilitud. Existen diferentes maneras de calcular la similitud, la distancia o la disimilitud de dos puntos de datos. El más común es la distancia de Euclidia.
Funcionamiento (VER EJEMPLO EN PYTHON)
En un problema de clasificación, el algoritmo del vecino más próximo funciona de la siguiente forma:
- Elegir un valor para K.
- Calcular la distancia desde el nuevo caso (exclusión de cada uno de los casos del conjunto de datos).
- Buscar las «k» observaciones en los datos de entrenamiento que son «más próximos» al punto de datos desconocido.
- Predecir la respuesta del punto de datos desconocido utilizando el valor de respuesta más popular de los vecinos más próximos.
Hay dos partes en este algoritmo que pueden ser un poco confusas: Cómo seleccionar la K correcta y cómo calcular la similaridad entre los casos.
Calculo de similitud
Se puede utilizar la distancia Minkowski para calcular la distancia entre datos, que es en efecto, la distancia Euclidia: 
Si tenemos más de una característica podemos seguir utilizando la misma fórmula, pero ahora lo usamos en un espacio bidimensional. También podemos usar la misma matriz de distancia para los vectores multidimensionales. Por supuesto, tenemos que normalizar nuestro conjunto de características para obtener la medida de disimilitud precisa. También hay otras medidas de disimilitud que pueden ser utilizadas para este propósito, pero, tal como se menciona, es altamente dependiente del tipo de datos y también el dominio que la clasificación está hecho por él.
Cálculo de K en el k-vecinos más próximos
En el algoritmo de K-vecinos más próximos, K es el número de vecinos más próximos a examinar. Se supone que debe ser especificado por el usuario.
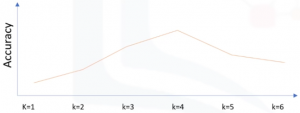
¿Qué ocurre si elegimos un valor muy bajo de K, digamos, k= 1? Esto sería una mala predicción, ya que un caso específico puede hacer que el modelo falle. Podemos decir que hemos capturado el ruido en los datos, o elegimos uno de los puntos que era una anomalía en los datos. Un valor bajo de K causa también un modelo muy complejo, lo que podría resultar en un exceso de ajuste del modelo. Esto significa que el proceso de predicción no se generaliza lo suficiente como para ser utilizado para casos fuera de la muestra. Los datos de fuera de la muestra son datos que están fuera del conjunto de datos utilizado para entrenar el modelo. En otras palabras, no se puede confiar en que sea utilizado para la predicción de muestras desconocidas. Es importante recordar que el exceso de ajuste es malo, ya que queremos un modelo general que funcione para cualquier dato, no sólo los datos utilizados para el entrenamiento.
Ahora, en el lado opuesto del espectro, si elegimos un valor muy alto de K, tal como K=20, entonces el modelo se vuelve demasiado generalizado. Así que, ¿cómo podemos encontrar el mejor valor para K? La solución general es reservar una parte de los datos para probar la precisión del modelo. Una vez que se ha hecho, se elige k =1, y luego se usa la parte de entrenamiento para modelaje, y calcula la precisión de la predicción utilizando todos los ejemplos en el conjunto de pruebas. Se repite este proceso, incrementando el k, y se ve cuál de los k es el mejor para su modelo.
El análisis del vecinos más próximo también se puede utilizar para calcular valores para un objetivo continuo. En esta situación, se utiliza el valor de objetivo promedio o promedio de los vecinos más próximos para obtener el valor predicho para el nuevo caso. Por ejemplo, suponga que está prediciendo el precio de un inicio basado en su conjunto de características, tales como el número de habitaciones, las imágenes cuadradas, el año en que fue construido, etc. Puede encontrar fácilmente las tres casas vecinas más cercanas, por supuesto, no sólo en base a la distancia, si no también basado en todos los atributos, y luego predice el precio de la casa, como el promedio de los vecinos.
Ir al artículo anterior de la serie: Introducción a la clasificación
Ir al artículo siguiente de la serie: Evaluación del modelo de clasificación
