Evaluación del modelo de clasificación
Las métricas de evaluación del modelo de clasificación explican el rendimiento de un modelo. Para mostrar algunos modelos de evaluación para la clasificación, vamos a utilizar el supuesto de un conjunto de datos que muestra el ratio de abandono de clientes de una Empresa. Hemos entrenado al modelo,y ahora queremos calcular su precisión utilizando el set de pruebas. Pasamos el set de pruebas a nuestro modelo,y encontramos las etiquetas predichas. ¿Cómo de preciso es este modelo?
Básicamente, se comparan los valores reales del conjunto de pruebas con los valores pronosticados por el modelo, para calcular su precisión. Las métricas de evaluación del modelo de clasificación proporcionan un papel clave en el desarrollo de un modelo, ya que proporcionan pistas de las áreas que pueden mejorarse. Hay diferentes métricas de evaluación de modelos, pero vamos a evaluar las más usadas: índice de Jaccard, F1-score y Log Loss.
Índice de Jaccard
Es una de las medidas de precisión más simples, y también es conocido como el coeficiente de similaridad Jaccard. Para el cálculo de este índice se utiliza la teoría de conjuntos y se puede definir como la intersección de los conjuntos de valores predichos y reales dividido por unión de los dos conjuntos de datos. Si el conjunto completo de etiquetas predichas para una muestra coincide estrictamente con el conjunto verdadero de etiquetas, entonces la precisión del es 1.0, en el extremo contrario, si no coincide ningún valor, el índice es 0.0.
Matríz de confusión (F1-score)
La matriz de confusión muestra las predicciones correctas y exhaustivas, en comparación con las etiquetas reales. Cada fila de la matriz de confusión muestra las etiquetas Reales/Verdaderas del conjunto de pruebas, y las columnas muestran las etiquetas predichas por el clasificador. La matriz de confusión muestra la habilidad del modelo para predecir correctamente. En el caso específico de un clasificador binario podemos interpretar estos números como el recuento de positivos verdaderos (aciertos), positivos falsos (errores), negativos verdaderos (errores), y negativos falsos (aciertos). Basándonos en el conteo de cada sección, podemos calcular la precisión y la exhaustividad de cada una de las etiquetas. La precisión es una medida de la exactitud, a condición de que una etiqueta de clase se haya predicho correctamente.
Se define mediante:
![]()
![]()
![]()
![]()
Por lo tanto, podemos calcular la precisión y la exhaustividad de cada clase y con ello el F1-scores para cada etiqueta: El F1-score es el promedio armónico de la precisión y la exhaustividad, donde el F1-score alcanza su mejor valor en 1 (que representa la precisión y la exhaustividad perfecta) y su peor valor en 0. Se define utilizando la ecuación F1-score: ![]()
![]()
Supongamos el siguiente ejemplo:
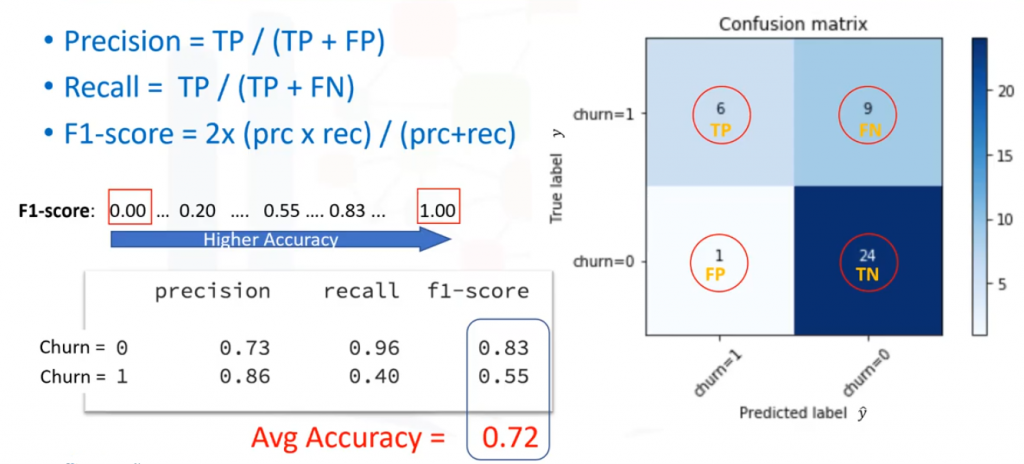

Para el valor churn=0, ![]()
![]()
![]()
![]()
![]()
![]()
Para el valor churn=1, ![]()
![]()
![]()
![]()
![]()
![]()
Y finalmente la media ponderada es ![]()
![]()
Tenga en cuenta que tanto Jaccard como F1-score se pueden utilizar también para clasificadores multi-clase.
Log Loss
A veces, el resultado de un clasificador es la probabilidad de una etiqueta de clase, en lugar de la etiqueta. Por ejemplo, el resultado puede ser la probabilidad de abandono del cliente, es decir, si el resultado es 1, entonces el cliente abandonaría. Esta probabilidad es un valor entre 0 y 1. Log loss mide el rendimiento de un clasificador donde el resultado pronosticado es un valor de probabilidad entre 0 y 1.
Se puede calcular el Log loss para cada fila utilizando la ecuación de Log loss, que mide como de lejos está cada predicción con respecto a la etiqueta real. Luego calculamos el Log loss promedio en todas las filas del conjunto de pruebas:
![]()
![]()
Es evidente que los clasificadores más idóneos tienen valores progresivamente más pequeños de Log loss. Por lo tanto, el clasificador con menor Log loss tiene una mejor precisión.
Ir al artículo anterior de la serie: K-vecinos más próximos
Ir al artículo siguiente de la serie: Introducción a los árboles de decisión