Regresión lineal simple

Regresión lineal simple

La pregunta que trata de responder la regresión linea simple es: Dado un conjunto de datos, ¿Podemos predecir una de las variables, utilizando otro campo?
La respuesta es sí: Podemos utilizar la regresión lineal para predecir un valor continuo utilizando otras variables. La regresión lineal es la aproximación de un modelo lineal que se utiliza para describir la relación entre dos o más variables. En la regresión lineal simple, hay dos variables: una variable dependiente y una variable independiente. El punto clave en la regresión lineal es que nuestro valor dependiente debe ser continuo y no puede ser un valor discreto. Sin embargo, las variables independientes pueden ser medidas en una escala de medida categórica o continua.

Existen dos tipos de modelos de regresión lineal: regresión simple y regresión múltiple.La regresión lineal simple es cuando se utiliza una variable independiente para estimar una variable dependiente. Cuando se utiliza más de una variable independiente, el proceso se denomina regresión lineal múltiple.

La mejor manera de entender la regresión lineal es dibujando nuestras variables. Vamos a usar el tamaño del motor 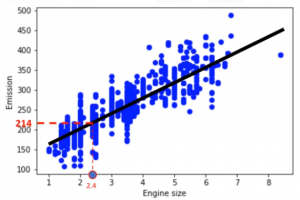regresión lineal simplecomo una variable independiente, y la Emisión como el valor objetivo que queremos predecir. Un diagrama de dispersión muestra la relación entre estas variables. Además, se ve que estas variables están relacionadas linealmente. Con la regresión lineal, se puede ajustar una línea a través de los datos.

La línea de ajuste se muestra tradicionalmente como un polinomio. En un problema de regresión simple (una sola variable independiente), la forma del modelo sería y = \theta_0 + \theta_1 \cdot x_1. En esta ecuación, «y» es la variable dependiente (valor pronosticado), x_1 es la variable independiente, \theta_1 es conocida como «pendiente» y el valor \theta_0 se conoce como  «ordenada en el origen». \theta_0 y \theta_1 son los coeficientes de la ecuación lineal.

Calculo de los coeficientes

Ahora la preguntas es ¿Cómo se determina cuál de las líneas «encaja mejor»? ¿Cómo calcular \theta_0 y \theta_1 para encontrar la mejor línea para «ajustar» los datos?.
Supongamos que ya hemos encontrado la mejor línea de ajuste para nuestros datos. Solo nos faltaría comprobar lo bien que se ajustan los datos reales con esta línea. Esto significa que si para un elemento de la muestra tenemos un valor de la variable independiente, la variabe dependiente calculada debe aproximarse muy cerca del valor real. Esto no suele ser así, ya que siempre suele existir un error, y esto significa que nuestra línea de predicción no es precisa. Este error se denomina error residual.

Podemos decir que el error es la distancia desde el punto de datos hasta la línea de regresión ajustada y que la media de todos los errores residuales muestra lo mal que encaja la línea con todo el conjunto de datos. Matemáticamente, es calculado por la ecuación del error de cuadrado medio (ECM), o en inglés «mean squared error» (MSE). El objetivo es encontrar una línea en la que se minimice la media de todos estos errores.

    \[ MSE=\frac{1}{n}\sum_{i=1}^{n}{(y_i-y'_i)^2} \]

Podemos utilizar unas fórmulas matemáticas para calcular \theta_0 y \theta_1:

\theta_1 = \frac{\sum_{i=1}^{s}{(x_i -\overline{x}) \cdot (y_i -\overline{y})}}{\sum_{i=1}^{s}{(x_i -\overline{x})^2}}

\theta_0 = \overline{y} - \theta_1 \cdot \overline{x}

Se requiere que calculemos la media de las columnas independientes y dependientes de todo el conjunto de datos, por lo que todos los datos deben estar disponibles. Una vez calculada la media, se estima el valor de \theta_1 y luego con ese valor calcular \theta_0.

Realmente no necesitas recordar la fórmula para el cálculo de estos parámetros, la mayoría de las librerias usadas para el aprendizaje automático en Python, R, y Scala pueden encontrar fácilmente estos parámetros. Pero siempre es bueno entender cómo funciona. (VER EJEMPLO EN PYTHON)

Después de que encontramos los parámetros de la ecuación lineal, hacer predicciones es tan simple como solucionar la ecuación para un conjunto específico de entradas.

Utilidad de la regresión lineal simple

La regresión lineal es la más básica que hay que utilizar y entender. Es muy útil, ya que es rápida y no requiere ajuste de parámetros como ocurre en otros cálculos de predicción donde hay que ajustar el parámetro K en los K-Vecinos mas cercanos o la tasa de aprendizaje en las Redes Neuronales. La regresión lineal también es fácil de entender y altamente interpretables.

Ir al artículo anterior de la serie: Introducción al Modelo de Regresión

Ir al artículo siguiente de la serie: Regresión lineal múltiple

Artículos relacionadosMás del autor

DEJA UNA RESPUESTA

Por favor ingrese su comentario!
Por favor ingrese su nombre aquí