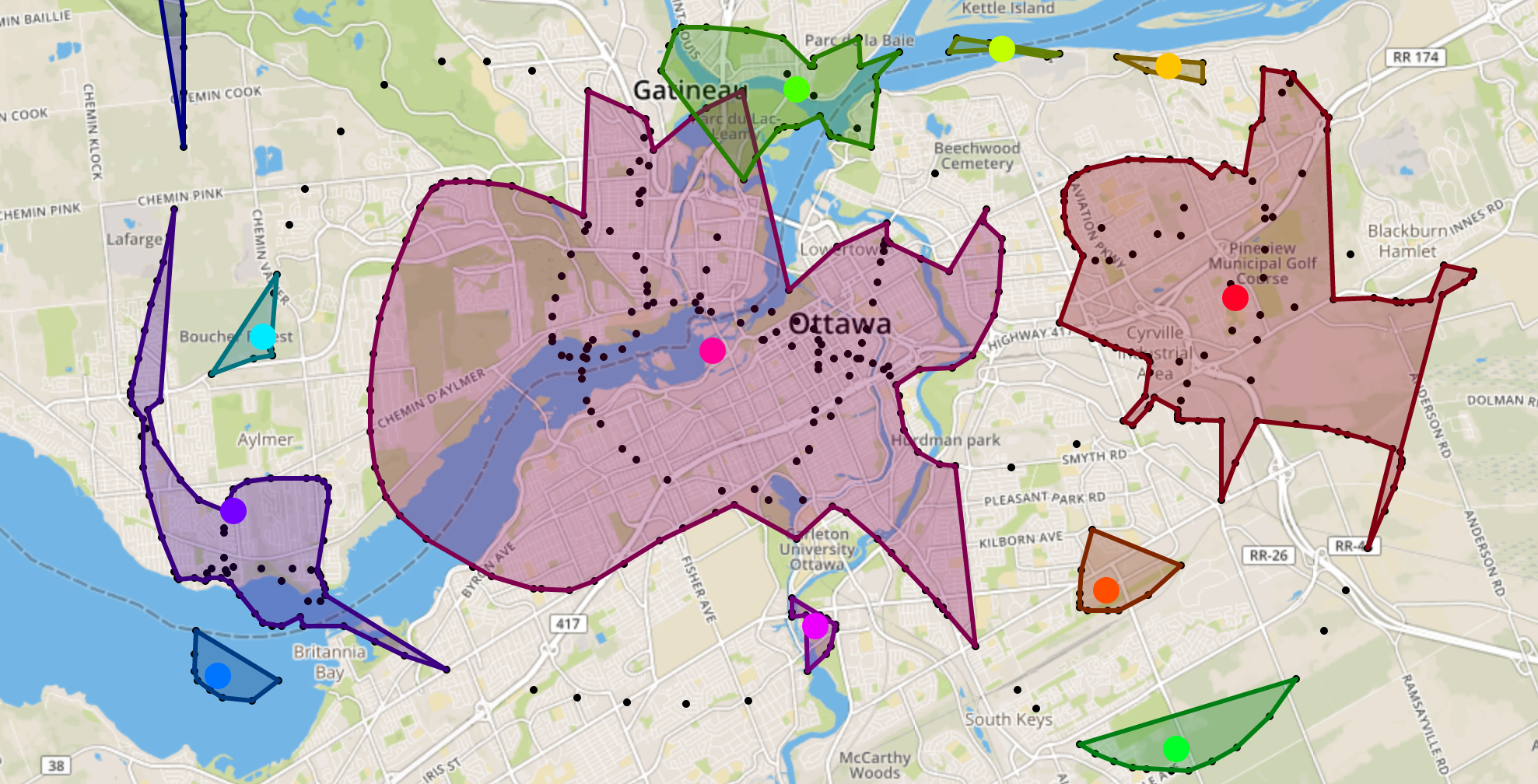
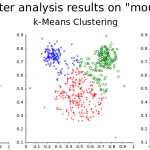
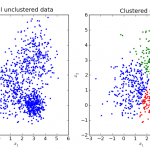
Agrupación por K-medias en Python
Existen muchos modelos para clustering. En este ejemplo vamos a usar el K-medias, que se utiliza mucho en ciencia de datos, especialmente si se...
Introducción al clustering
Introducción al clustering
Vamos a ver una introducción al clustering, sus aplicaciones y diferentes tipos de algoritmos.
Imaginemos que tenemos un conjunto de datos y necesitamos...
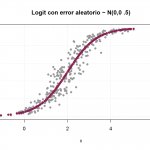
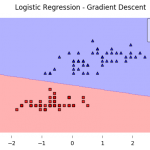
Cálculo de los parámetros de la función logística
Cálculo de los parámetros de la función logística
El objetivo principal es el cálculo de los parámetros de la función logística para que sea la...
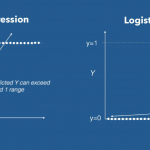
Regresión lineal Vs. regresión logística
Regresión lineal Vs. regresión logística
Vamos a ver la diferencia entre la regresión lineal vs. la regresión logística. Revisaremos la regresión lineal y veremos por...
Introducción a la Regresión Logística
¿Que es regresión logística?
La regresión logística es una técnica estadística de machine learning para clasificar los registros de un conjunto de datos, basandose en...
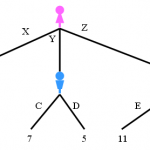
Construyendo árboles de decisión
Construyendo árboles de decisión
Vamos a ver como se están construyendo los árboles de decisión: se crean utilizando el particionamiento recursivo para clasificar los datos....
Introducción a los árboles de decisión
Introducción a los árboles de decisión
Para ver una introducción a los árboles de decisión, imagina que eres un investigador médico que compila datos para...
Evaluación del modelo de clasificación
Evaluación del modelo de clasificación
Las métricas de evaluación del modelo de clasificación explican el rendimiento de un modelo. Para mostrar algunos modelos de evaluación...
K-vecinos más próximos en Python
Importación de los paquetes básicos
import itertools
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
import pandas as pd
import numpy as np
import matplotlib.ticker as ticker
from...
K-vecinos más próximos
K-vecinos más próximos
Para comprender el algorítmo de clasificación K-vecinos más próximos, imagine que un proveedor de telecomunicaciones ha segmentado su base de clientes según...