K-vecinos más próximos en Python
Importación de los paquetes básicos
import itertools
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
import pandas as pd
import numpy as np
import matplotlib.ticker as ticker
from...
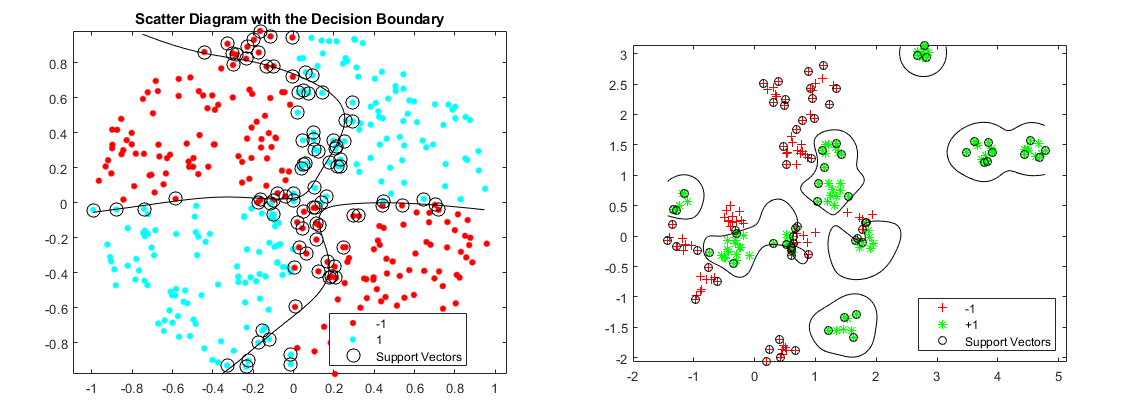
K-vecinos más próximos
K-vecinos más próximos
Para comprender el algorítmo de clasificación K-vecinos más próximos, imagine que un proveedor de telecomunicaciones ha segmentado su base de clientes según...
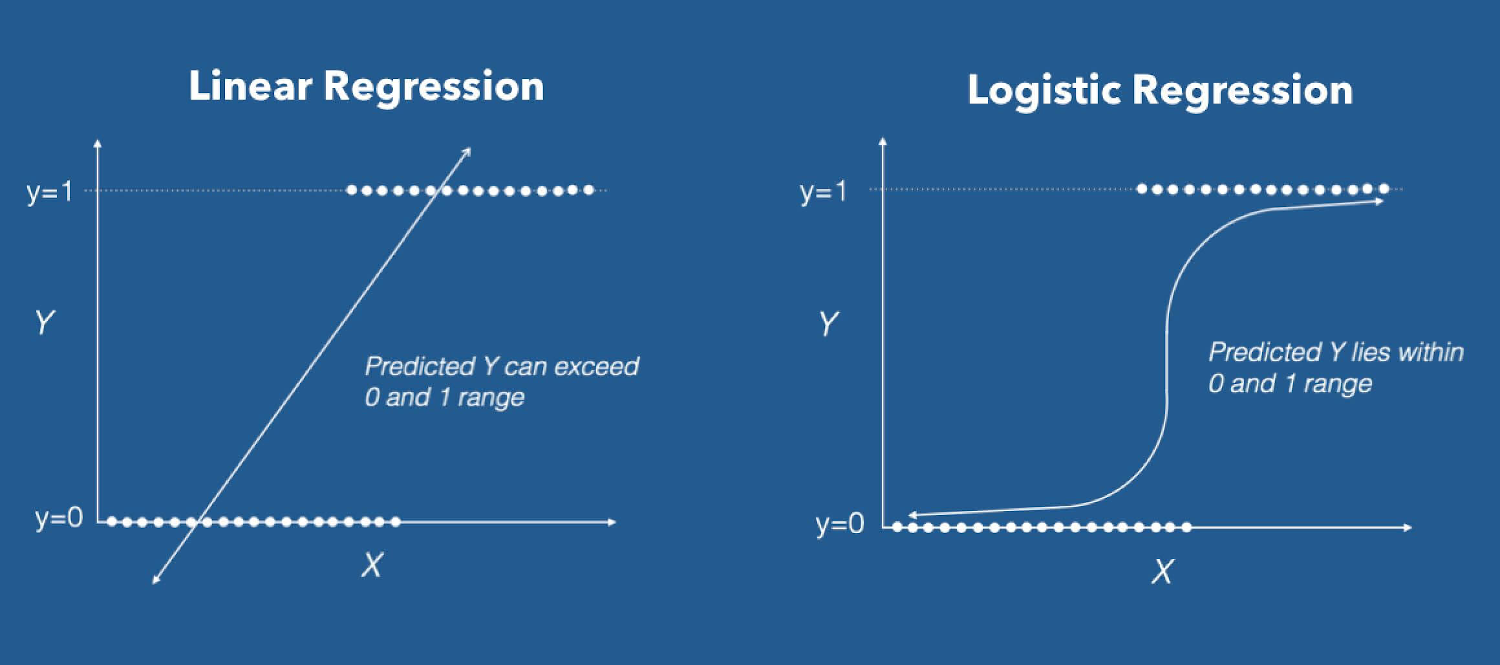
Introducción a la clasificación
Introducción a la clasificación
Para realizar esta introducción a la clasificación tenemos que conocer que en Machine Learning, la clasificación es un enfoque de aprendizaje...