Introducción a los sistemas de recomendación
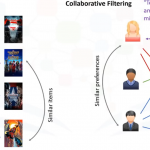
Introducción a los sistemas de recomendación.
A pesar de que los gustos de los personas pueden variar, en general siguen patrones. Con eso, quiero decir...
Clustering DBSCAN
Clustering DBSCAN
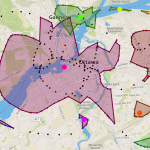
DBSCAN es un algoritmo de clustering basado en la densidad, que es apropiado utilizar al examinar datos espaciales.
La mayoría de las técnicas tradicionales...
Agrupación en clúster jerárquica en Python
Clustering Jerárquico - Aglomerativo
Vamos a ver la técnica de Clustering Jerárquico Aglomerativo. Es un enfoque de abajo hacia arriba (bottom up). Este enfonque es...
Agrupación en clúster jerárquica
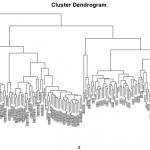
Agrupación en clúster jerárquica
En el gráfico adjunto vemos un dendrograma de agrupación en clúster jerárquica para reportar datos genéticos de más de 900 perros...
Agrupación por K-medias en Python
Existen muchos modelos para clustering. En este ejemplo vamos a usar el K-medias, que se utiliza mucho en ciencia de datos, especialmente si se...
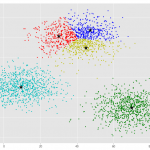
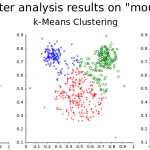
Agrupación por K-medias
Agrupación por K-medias.
Existen varios tipos de algoritmos de agrupación, tales como agrupaciones basadas en particiones, basadas en jerarquías o basadas en densidades. K-medias es...
Introducción al clustering
Introducción al clustering
Vamos a ver una introducción al clustering, sus aplicaciones y diferentes tipos de algoritmos.
Imaginemos que tenemos un conjunto de datos y necesitamos...
Máquinas de soporte de vectores en Python
Vamos a utilizar Máquinas de Soporte de Vectores (SVM) (Support Vector Machines) para construir y entrenar un modelo utilizando registros de células humanas para...
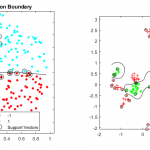
Máquinas de soporte de vectores
Máquinas de soporte de vectores
Las máquinas de soporte de vectores (SVM - Support Vector Machine) es un algoritmo supervisado que puede clasificar los casos...
Regresión logística en Python
Vamos a crear un modelo basado en datos de telecomunicaciones para predecir cuándo los clientes buscarán otro competidor de tal forma que podamos tomar...