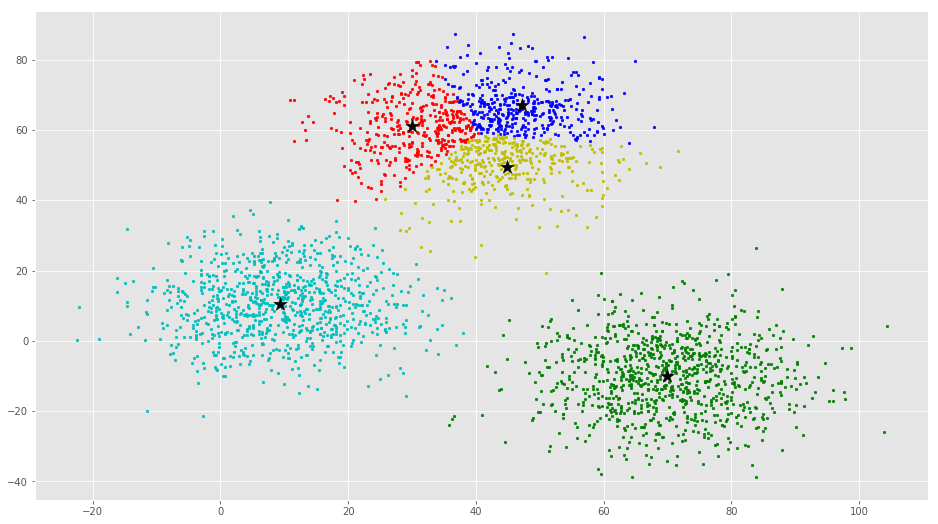
Agrupación por K-medias

Agrupación por K-medias.

Existen varios tipos de algoritmos de agrupación, tales como agrupaciones basadas en particiones, basadas en jerarquías o basadas en densidades. K-medias es una agrupación basada en particiones, es decir, divide los datos en subconjuntos no solapados (o particiones) sin ninguna estructura interna. Esto significa, que es un algoritmo no supervisado. Los objetos dentro de una partición serán muy similares y los objetos de las distintas particiones serán muy diferentes o disimilares. Como puede verse, para usar K-medias, tenemos que encontrar muestras similares.

Aunque el objetivo de K-medias es formar particiones de tal manera que muestras similares vayan a una partición y muestras disimilares caígan en diferentes particiones, se puede demostrar que en lugar de una métrica de similitud, podemos utilizar métricas de disimilitud. En otras palabras, la distancia de las muestras entre sí se utiliza para moldear las particiones. Así que, podemos decir que K-medias trata de minimizar las distancias «intra-partición» y maximiza las distancias «inter-partición».

Para calcular la disimulitud o la distancia de dos puntos, podemos utilizar un tipo específico de distancia de Minkowski, la distancia Euclidiana.

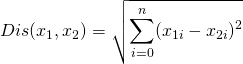
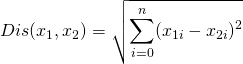
Por supuesto, tenemos que normalizar nuestro conjunto de características para obtener la medida de disimilitud precisa. También hay otras medidas de disimilitud que pueden ser utilizadas para este propósito, pero dependen en gran medida del tipo de datos y también del dominio para el cual se ha hecho la partición. Por ejemplo, se puede utilizar la distancia euclidiana, la similitud del coseno, la distancia promedio, etc… De hecho, la medida de similitud controla grandemente cómo se forman las particiones, por lo que se recomienda comprender el conocimiento de dominio de tu conjunto de datos y el tipo de datos de las características y después seleccionar la medida de distancia significativa.

Funcionamiento de la agrupación por K-medias

Lo primero es determinar el número de particiones que buscamos. El concepto clave del algoritmo K-medias es que escoge aleatoriamente un punto central para cada partición. Esto significa que tenemos que inicializar ‘k’, la cual representa «el número de particiones». Determinar el número de particiones en un conjunto de datos, o ‘k’, es un problema difícil en K-medias. Por ahora, vamos a proponer que ‘k’ sea igual a 3, así que tendremos 3 puntos representativos para nuestras particiones. Estos 3 puntos de datos se denominan centroides de las particiones, y deben ser del mismo tamaño que la característica de nuestro conjunto de características de cliente. Hay dos enfoques para elegir estos centroides:

1. Podemos elegir aleatoriamente 3 observaciones fuera del conjunto de datos y utilizar estas observaciones como los medios iniciales.
2. Podemos crear 3 puntos aleatorios como centroides de las particiones.

Después del paso de inicialización, que define el centroide de cada partición, tenemos que asignar cada observación al centroide más cercano. Con este fin, tenemos que calcular la distancia de cada punto de datos de los centroides. Como se ha mencionado antes, en función de la naturaleza de los datos y de la finalidad para la que el particionamiento es realizado, se pueden utilizar diferentes medidas de distancia para colocar los elementos en particiones. Por lo tanto, se formará una matriz en la que cada fila representa la distancia de una observación a cada centroide. Esta matriz se llama la «matriz de distancia».

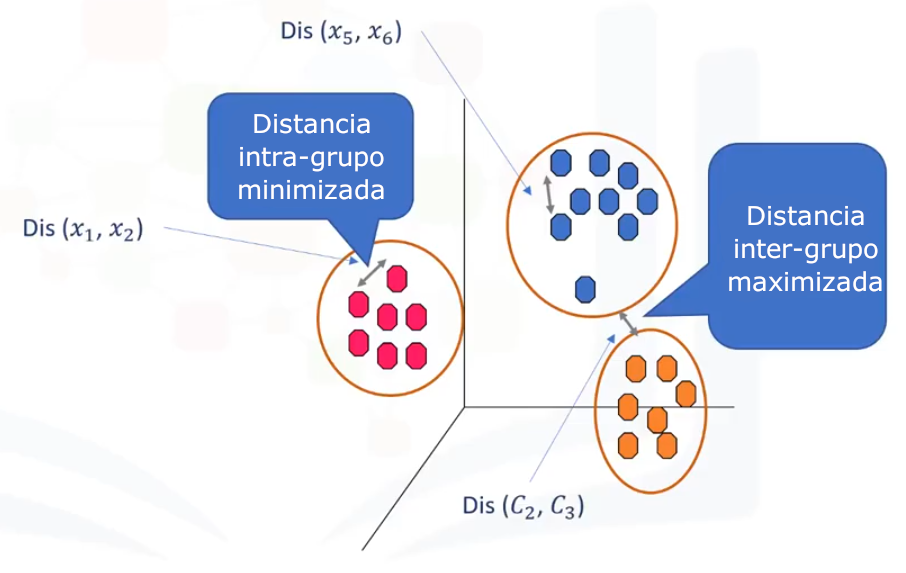
El objetivo principal de la agrupación K-medias es minimizar la distancia de los puntos de datos al centroide de su partición y maximizar la distancia hacía los centroides de las otras particiones. Por lo tanto, en este paso tenemos que encontrar el centroide más cercano a cada punto de datos. Podemos utilizar la matriz de distancia para encontrar el centroide más cercano a los puntos de datos. Encontrando los centroides más cercanos para cada punto de datos, asignamos cada punto de datos a dicha partición. En otras palabras, todos los clientes caerán en una partición, basándose en su distancia hacía los centroides. Facilmente podemos decir que este procedimientos no logra buenas particiones, porque los centroides fueron escogidos al azar inicialmente. De hecho, el modelo tendá un gran error. Aquí,el error es la distancia total de cada punto a su centroide. Se puede mostrar como un error de la suma de los cuadrados dentro de una partición.

Intuitivamente, vamos a tratar de reducir este error. Debemos dar forma a las particiones de tal manera que la distancia total de todos los miembros
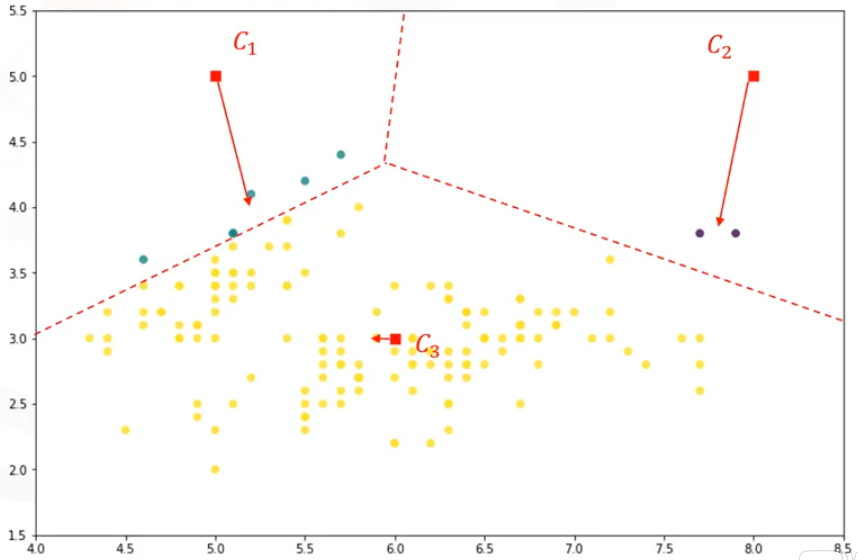
de una partición a su centroide se minimicen. Así que movemos los centroides para que sean la media de los puntos de datos de su partición. De hecho, cada centroide se mueve de acuerdo con los miembros de su partición. En otras palabras, el centroide de cada uno de los 3 grupos se convierte en la nueva media. Ahora tenemos nuevos centroides. Como puedes adivinar, una vez más, tendremos que calcular la distancia de todos los puntos a los nuevos centroides. Los puntos se vuelven a agrupar y los centroides se mueven de nuevo. Esto continúa hasta que los centroides ya no se muevan.

Sí, K-medias es un algoritmo iterativo, y tenemos que repetir los pasos hasta que el algoritmo converja. En cada iteración, moverá los centroides, calculará las distancias de los nuevos centroides, y asignará los puntos de datos al centroide más cercano. Esto resulta en particiones con un error mínimo, o particiones más consistentes. Sin embargo, como se trata de un algoritmo heurístico, no es garantía de que converja a la óptima global, y el resultado pueda depender de las particiones iniciales. Esto significa que este algoritmo está garantizado para converger a un resultado, pero el resultado puede ser un óptimo local (es decir, no necesariamente el mejor resultado posible). Para solucionar este problema, es común que se ejecute todo el proceso varias veces, con diferentes condiciones de partida. Esto significa, que con centroides iniciales aleatorizados, se puede obtener un mejor resultado. Y como el algoritmo es usualmente muy rápido, no sería ningún problema ejecutarlo varias veces.
Puedes ver un ejemplo en este artículo: Agrupación por K-medias en Python

Ir al artículo anterior de la serie: Introducción al clustering

Ir al artículo siguiente de la serie: Agrupación en clúster jerárquica