Agrupación en clúster jerárquica
En el gráfico adjunto vemos un dendrograma de agrupación en clúster jerárquica para reportar datos genéticos de más de 900 perros de 85 razas y más de 200 lobos grises salvajes de alrededor del mundo, incluyendo poblaciones de norte América, Europa, Oriente Medio y Asia Oriental. Se usaron técnicas para analizar más de 48,000 marcadores genéticos. Este diagrama muestra la agrupación jerárquica de estos animales en función de la similitud en sus datos genéticos.
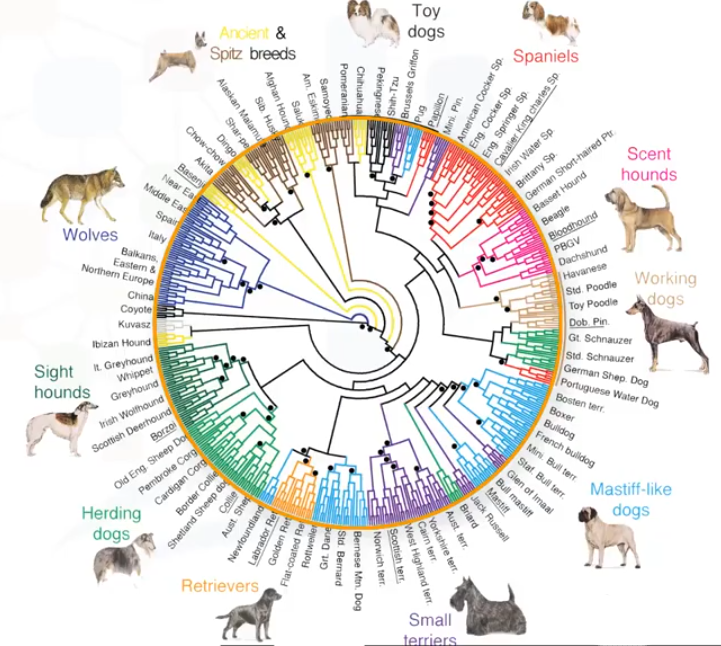
Los algoritmos de clústeres jerárquicos construyen una jerarquía de clústeres en el que cada nodo es un clúster que consta de los clústeres de sus nodos hijas. Las estrategias para la agrupación jerárquica en general se dividen en dos tipos: Divisivo y Aglomerativo. La división es descendente, por lo que se inicia con todas las observaciones en un clúster grande y se dividen en partes más pequeñas. Imagina divisivo como «dividir» el clúster. El aglomerativo es lo contrario de divisivo, por lo que es de abajo hacia arriba, donde cada observación se inicia en su propio clúster y los pares de clústeres se fusionan a medida que avanzan en la jerarquía. La aglomeración significa manipular o recoger cosas, que es exactamente lo que esto hace con el clúster.
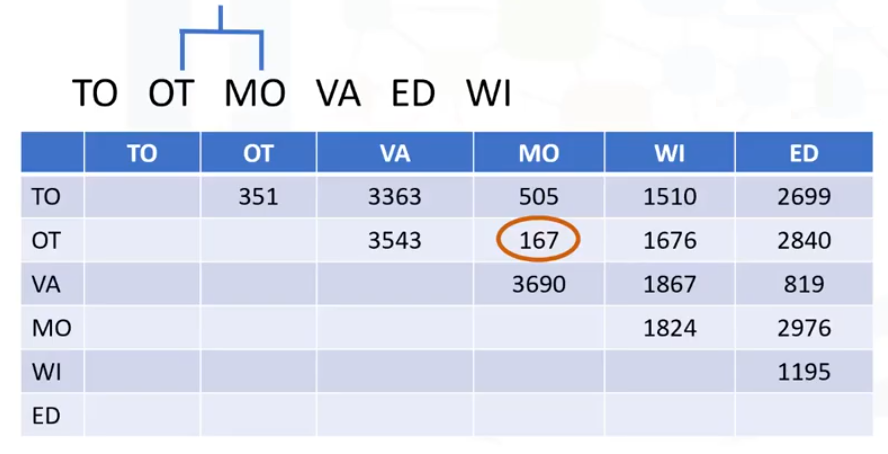
El enfoque aglomerativo es más popular entre los «Data Scientists», por lo que vamos a verlo en esta entrada. Este método construye la jerarquía a partir de los elementos individuales mediante la fusión progresiva de clústeres. Vamos a ver un ejemplo en el que queremos agrupar 6 ciudades en Canadá basados en sus distancias unas de otras. Estos son: Toronto, Ottawa, Vancouver, Montreal, Winnipeg y Edmonton. Construimos una matriz de distancias donde los números de la fila i columna j son la distancia entre las ciudades. El algoritmo se inicia mediante la asignación de cada ciudad a su propio clúster. Así que, como tenemos 6 ciudades, tenemos 6 grupos, cada uno conteniendo sólo una ciudad. El primer paso es determinar qué ciudades (o grupos) se fusionan en un clúster. Para esto se seleccionan los dos clústers más cercanos según la distancia elegida. Mirando la matriz de distancia, Montreal y Ottawa son los clústers más cercanos. Así que, creamos un cluster de ellos. Sólo hemos usado una función de distancia unidimensional, pero nuestro objeto puede ser multidimensional, y la medición de distancia puede ser Euclidiana, Pearson, distancia promedio, o muchas otras, en función del tipo de datos y del conocimiento del dominio.
Como se puede ver en la matriz de distancia, las filas y las columnas relacionadas con las ciudades de Montreal y Ottawa se fusionan a medida que se construye el clúster. En consecuencia, las distancias de todas las ciudades a este nuevo clúster fusionado se actualizan. Seleccionamos la distancia desde el centro del clúster de Otawa-Montreal hacia Winnipeg. Actualizando la matriz de distancia, ahora tenemos un clúster menos. A continuación, buscamos los clústeres más cercanos una vez más. En este caso, Ottawa-Montreal y Toronto son los más cercanos, lo que crea otro clúster. En el siguiente paso, la distancia más cercana es entre el clúster de Vancouver y el clúster de Edmonton Formando un nuevo clúster, sus datos en la matriz la tabla se actualizan. Esencialmente, las filas y las columnas se fusionan a medida que se fusionan los clústeres y se actualiza la distancia.
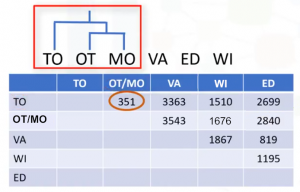
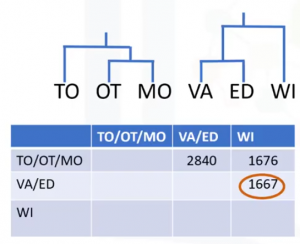
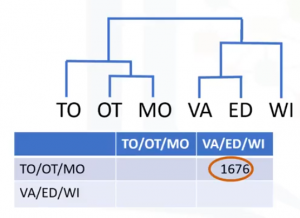
Esta es una forma común de implementar este tipo de clustering, y tiene el beneficio de almacenar caché de las distancias entre clústeres. De la misma manera, el algoritmo aglomerativo procede luego de una fusión de clústeres. Y lo repetimos hasta que todos los clústeres se fusionen y el árbol se complete, esto es, hasta que todas las ciudades están agrupadas en un solo clúster de tamaño 6. La agrupación jerárquica se visualiza normalmente como un dendrograma tal como se muestra en esta imagen. Cada fusión se representa mediante una línea horizontal. Al subir desde la capa inferior hasta el nodo superior, un dendrograma nos permite reconstruir el historial de fusiones que ha resultado en la agrupación en clústeres representados.
Cálculo de la proximidad
El primer paso es crear n clusteres, uno para cada punto de datos. A continuación, cada punto se asigna como un cluster. Luego claculamos la matriz de distancia/proximidad, que será n por n en la primera tabla. Después ejecutamos de forma iterativa ejecutamos la «unión» de los dos grupos más cercanos y actualizamos la matriz de proximidad con los nuevos valores. Nos detenemos después de que hayamos alcanzado el número especificado de clusteres, o sólo hay un cluster que queda, con el resultado almacenado en un dendrograma. Así que, en la matriz de proximidad, tenemos que medir las distancias entre clusteres, y también fusionar los clusteres que son «más cercanos». Por lo tanto, la operación clave es la computación de la proximidad entre los clusteres con un punto, y también clusteres con varios puntos de datos.
Podemos usar diferentes medidas de distancia para calcular la matriz de proximidad. Por ejemplo, la distancia euclidiana. Así que si tenemos un conjunto de datos de n observaciones, podemos construir una matriz de n por n distancia. Ésta nos dará la distancia de las agrupaciones con 1 punto de datos. Sin embargo, fusionamos los grupos en clustering aglomerativo, por lo que la distancia entre los clusteres se debe calcular con varias observaciones. Para ello podemos utilizar diferentes criterios. En general, depende completamente del tipo de datos, la dimensionalidad de los datos, y lo más importante, el conocimiento de dominio del conjunto de datos. De hecho, diferentes enfoques a la hora de definir la distancia entre clusteres, nos dan diferentes resultados. Podemos ver algunos:
- Clustering de enlace único. El enlace único se define como la distancia más corta entre 2 puntos en cada cluster.
- Complete-Linkage Clustering. Esta vez, estamos encontrando la distancia más larga entre los puntos de cada cluster.
- Clustering promedio de enlaces, o la distancia media. Esto significa que estamos tomando la distancia promedio de cada punto de un cluster a cada uno de los puntos de otro cluster.
- Clustering de enlaces centroide. Centroide es el promedio de los conjuntos de características de puntos en un cluster. Este enlace tiene en cuenta el centroide de cada cluster al determinar la distancia mínima.
Puedes ver un ejemplo en este artículo: Agrupación en clúster jerárquica en Python
Ventajas y desventajas
Hay 3 ventajas principales para utilizar el clustering jerárquico:
- No es necesario especificar el número de clusteres necesarios para el algoritmo.
- El clustering jerárquico es fácil de implementar.
- El dendrograma producido es muy útil para comprender los datos.
También hay algunas desventajas.
- El algoritmo nunca puede deshacer ninguna de los pasos anteriores. Si, por ejemplo, el algoritmo agrupa 2 puntos, y más tarde vemos que la conexión no era buena, el programa no puede deshacer ese paso.
- La complejidad del tiempo para el clustering puede dar lugar a tiempos de cálculo muy largos, en comparación con algoritmos eficientes, como K-Means.
- Si tenemos un conjunto de datos grande, puede ser difícil determinar el número correcto de clusteres por el dendrograma.
Comparación del clustering jerárquico con la k-Means.
- Los K-means son más eficientes para los conjuntos de datos grandes.
- El clustering jerárquico no requiere que se especifique el número de clusteres.
- El clustering jerárquico da más de un particionamiento en función de la resolución, mientras que k-Means sólo da un solo particionamiento de los datos.
- El clustering jerárquico siempre genera los mismos clusteres, en contraste con la k-Means que devuelve distintos clusteres cada vez que se ejecuta debido a la inicialización aleatoria de los centroides.
Ir al artículo anterior de la serie: Agrupación por K-medias
Ir al artículo siguiente de la serie: Clustering DBSCAN
